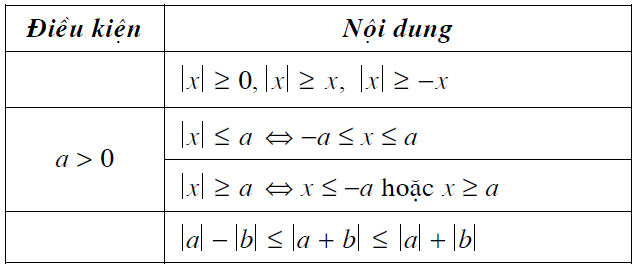I. Ôn tập bất đẳng thức

1. Khái niệm bất đẳng thức

Các mệnh đề dạng “a < b” hoặc a > b” được gọi là bất đẳng thức.

2. Bất đẳng thức hệ quả và bất đẳng thức tương đương

Nếu mệnh đề “$a < b \Rightarrow c < d$” đúng thì ta nói bất đẳng thức c < d là bất đẳng thức hệ quả của bất đẳng thức a < b và cũng viết là $a < b \Rightarrow c < d$.

Nếu bất đẳng thức a < b là hệ quả của bất đẳng thức c < d và ngược lại thì ta nói hai bất đẳng thức tương đương với nhau và viết là $a < b \Leftrightarrow c < d$.

3. Tính chất của bất đẳng thức

Tính chất của bất đẳng thức được tóm tắt trong bảng sau:

II. Bất đẳng thức giữa trung bình cộng và trung bình nhân (bất đẳng thức Cauchy (Cô-si))

1. Bất đẳng thức Cauchy

* Định lí

Trung bình nhân của hai số không âm nhỏ hơn hoặc bằng trung bình cộng của chúng.

$\sqrt {ab}  \le \frac{{a + b}}{2},\forall a,b \ge 0$ (1)

Đẳng thức $\sqrt {ab}  = \frac{{a + b}}{2}$ xảy ra khi và chỉ khi a = b.

2. Các hệ quả

* Hệ quả 1

Tổng của một số dương với nghịch đảo của nó lớn hơn hoặc bằng 2.

$a + \frac{1}{a} \ge 2,\forall a > 0$

* Hệ quả 2

Nếu x, y cùng dương và có tổng không đổi thì tích xy lớn nhất khi và chỉ khi x = y.

* Hệ quả 3

Nếu x, y cùng dương và có tổng không đổi thì tổng x + y nhỏ nhất khi và chỉ khi x = y.

III. Bất đẳng thức chứa dấu giá trị tuyệt đối