I. Các dạng phương trình của đường thẳng

1. Phương trình tham số của đường thẳng $\Delta $ qua điểm ${M_o}\left( {{x_o};{y_o};{z_o}} \right)$ có vectơ chỉ phương $\overrightarrow a  = \left( {{a_1};{a_2};{a_3}} \right)$ có dạng:

$\left\{ {\begin{array}{*{20}{l}}
{x = {x_o} + {a_1}t}\\
{y = {y_o} + {a_2}t}\\
{z = {z_o} + {a_3}t}
\end{array}} \right.,t \in R\,\,là\,\,tham\,\,số.$

2. Nếu $\left( {{a_1};{a_2};{a_3}} \right)$ khác không, ta viết phương trình trên ở dạng chính tắc:

$\frac{{x - {x_o}}}{{{a_1}}} = \frac{{y - {y_o}}}{{{a_2}}} = \frac{{z - {z_o}}}{{{a_3}}}.$


3. Phương trình tổng quát. Đường thẳng $d$ là giao tuyến của hai mặt phẳng:
$\left( P \right):{A_1}x + {B_1}y + {C_1}z + {D_1} = 0$ và
$\left( Q \right):{A_2}x + {B_2}y + {C_2}z + {D_2} = 0$
sẽ có phương trình tổng quát là
$\left\{ \begin{array}{l}
{A_1}x + {B_1}y + {C_1}z + {D_1} = 0\\
{A_2}x + {B_2}y + {C_2}z + {D_2} = 0
\end{array} \right.$

Khi đó vectơ chỉ phương của $d$ là ${\overrightarrow u _d} = \left[ {{{\overrightarrow n }_P},{{\overrightarrow n }_Q}} \right].$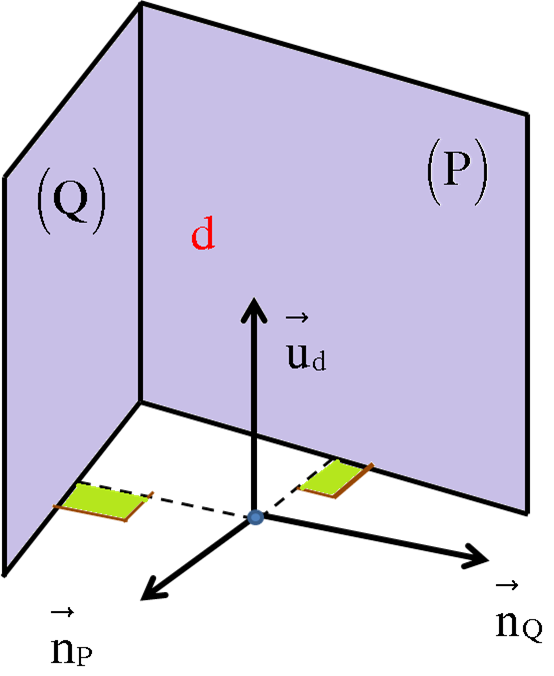


Ví dụ: Cho đường thẳng $\left( d \right)\left\{ \begin{array}{l}
2x + 3y + z - 6 = 0\\
x - y + 2z - 2 = 0
\end{array} \right.\left( * \right)$, hãy viết phương trình tham số và phương trình chính tắc

Giải

Ta có: ${\overrightarrow n _P} = \left( {2;3;1} \right),{\overrightarrow n _Q} = \left( {1; - 1;2} \right)$. Suy ra:
${\overrightarrow u _d} = \left[ {{{\overrightarrow n }_P},{{\overrightarrow n }_Q}} \right] = \left( {\left| \begin{array}{l}
3\\
 - 1
\end{array} \right.\left. \begin{array}{l}
1\\
2
\end{array} \right|; - \left| \begin{array}{l}
2\\
1
\end{array} \right.\left. \begin{array}{l}
1\\
2
\end{array} \right|;\left| \begin{array}{l}
2\\
1
\end{array} \right.\left. \begin{array}{l}
3\\
 - 1
\end{array} \right|} \right) = \left( {7; - 3; - 5} \right).$

Thay $x=1$ và (*) ta được $y=z=1 \Rightarrow A(1;1;1)  \in d.$

Phương trình tham số: 
$\left\{ {\begin{array}{*{20}{l}}
{x = 1 + 7t}\\
{y = 1 - 3t}\\
{z = 1 - 5t}
\end{array}} \right.,t \in R.$

Phương trình chính tắc:
$\frac{{x - 1}}{7} = \frac{{y - 1}}{{ - 3}} = \frac{{z - 1}}{{ - 5}}.$

II. Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau

1. Điều kiện để hai đường thẳng song song

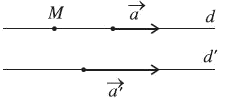
d song song với d’ khi và chỉ khi $\left\{ \begin{array}{l} \overrightarrow a  = k\overrightarrow a \\ M \notin d' \end{array} \right.$

Đặc biệt:

d trùng với d’ khi và chỉ khi $\left\{ \begin{array}{l} \overrightarrow a  = k\overrightarrow a \\ M \in d' \end{array} \right.$

2. Điều kiện để hai đường thẳng cắt nhau

Hai đường thẳng d và d’ cắt nhau khi và chỉ khi hệ phương trình ẩn t, t’ sau:

$\left\{ \begin{array}{l} {x_o} + t{a_1} = x{'_o} + t'{a_1}\\ {y_o} + t{a_2} = y{'_o} + t'{a_2}\\ {z_o} + t{a_3} = z{'_o} + t'{a_3} \end{array} \right.$

có đúng một nghiệm.

3. Điều kiện để hai đường thẳng chéo nhau

Hai đường thẳng d và d’ chéo nhau khi và chỉ khi $\overrightarrow a $ và $\overrightarrow a '$ không cùng phương và hệ phương trình

$\left\{ \begin{array}{l} {x_o} + t{a_1} = x{'_o} + t'a{'_1}\\ {y_o} + t{a_2} = y{'_o} + t'a{'_2}\\ {z_o} + t{a_3} = z{'_o} + t'a{'_3} \end{array} \right.$

vô nghiệm.