I. Định lí về dấu của tam thức bậc hai

1. Tam thức bậc hai

Tam thức bậc hai đối với x là biểu thức có dạng $f\left( x \right) = a{x^2} + bx + c$ trong đó a, b, c là những hệ số, $a \ne 0$.

2. Dấu của tam thức bậc hai

* Định lí

Cho $f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right),\Delta  = {b^2} - 4ac$

Nếu $\Delta $ < 0 thì f(x) luôn cùng dấu với hệ số a, với mọi $x \in R$.

Nếu $\Delta $ = 0 thì f(x) luôn cùng dấu với hệ số a, trừ khi $x = \frac{{ - b}}{{2a}}$.

Nếu $\Delta $ > 0 thì f(x) luôn cùng dấu với hệ số a khi x < x₁ hoặc x > x₂ trái dấu với hệ số a khi ${x_1} < x < {x_2}$ trong đó ${x_1},{x_2}\left( {{x_1} < {x_2}} \right)$ là hai nghiệm của f(x).

Minh họa hình học

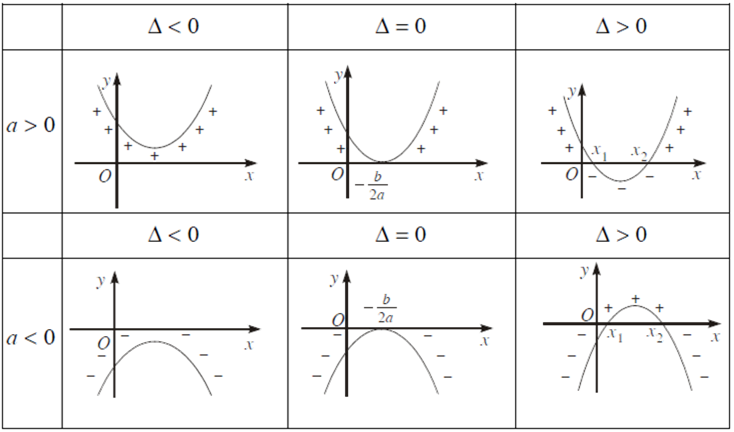
II. Bất phương trình bậc hai một ẩn

1. Bất phương trình bậc hai

Bất phương trình bậc hai ẩn x là bất phương trình dạng $a{x^2} + bx + c > 0$ (hoặc $a{x^2} + bx + c \le 0;a{x^2} + bx + c > 0;a{x^2} + bx + c \ge 0$), trong đó a, b, c là những số thực đã cho, $a \ne 0$.

2. Giải bất phương trình bậc hai

Giải bất phương trình bậc hai $a{x^2} + bx + c < 0$ thực chất là tìm các khoảng mà trong đó $a{x^2} + bx + c$ cùng dấu với hệ số a (trường hợp a < 0) hay trái dấu với hệ số a (trường hợp a > 0).