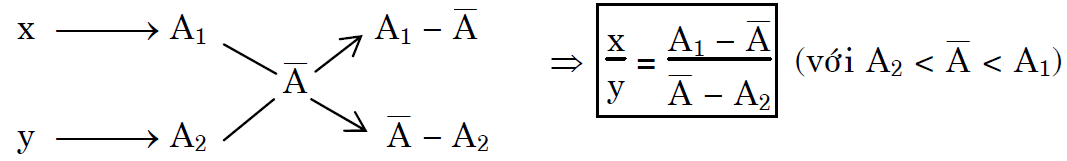1. Xác định nguyên tố khi biết tổng số hạt cơ bản
- Dựa vào biểu thức:
* Tổng số hạt: $P + E +N = 2P + N = a$ (số $p$ bằng số $e$) (1)
* Tỉ lệ (hoặc hiệu số) số hạt có điện và không điện: $\frac{{2P}}{N} = b\left( 2 \right)$
Giải hệ (1) và (2) suy ra $P$ và $N$ cũng như số khối $A$ của nguyên tử.
- Nếu không biết tỉ lệ số hạt có điện và không điện, ta dùng tỉ số nơtron và proton trong một nguyên tử (ngoại trừ $H$)
* Nếu $Z \le 20:1 \le \frac{N}{P} \le 1,333.$
* Nếu $Z > 20:1 \le \frac{N}{P} < 1,524.$
Kết hợp (1) ta có thể suy ra khoảng giá trị của $P$ (bằng số hiệu nguyên tử) và số khối tương ứng ($A=P+N$) $ \Rightarrow $ tên nguyên tố.
Ví dụ:
Hãy xác định nguyên tử có tổng số hạt là 82, biết tỉ số hạt mang điện và không mang điện là 15/13.
Hướng dẫn giải
Tổng số hạt $2P+N=82$ (1)
Ngoài ra: $\frac{{2P}}{N} = \frac{{15}}{{13}}\left( 2 \right)$
Từ (1) và (2) suy ra $P=26$ và $N=30$.
Số hiệu $Z=P=26$ (số khối $A=P+N=56$) ứng với nguyên tử $Fe$.
2. Tính % mỗi đồng vị theo quy tắc đường chéo
- Giả sử nguyên tử $A$ có nguyên tử khối trung bình $\overline A $, gồm 2 đồng vị có số khối ${A_1}$ (chiếm $x$%) và ${A_2}$ (chiếm $y$%), ta có:
Ví dụ:
$Cu$ có 2 đồng vị là ${}_{29}^{63}Cu$ và ${}_{29}^{65}Cu$ có nguyên tử khối trung bình là $63,54.$ Tính % số nguyên tử mỗi đồng vị.
Hướng dẫn giải
Gọi $x$ là % đồng vị ${}_{29}^{63}Cu$ và $y$ là % đồng vị ${}_{29}^{65}Cu$
Áp dụng công thức $\frac{x}{y} = \frac{{65 - 63,54}}{{63,54 - 63}} = \frac{{1,46}}{{0,54}} = \frac{{73}}{{27}}$
Suy ra $x = 73\% ;y = 27\% .$
3. Tính nguyên tử khối trung bình
- Một nguyên tử có thể có nhiều đồng vị với số khối ${A_i}$ khác nhau.
- Nguyên tử $X$ có $i$ đồng vị, số khối tương ứng là ${A_i}$ chiếm ${X_i}\% $ số nguyên tử, có nguyên tử khối trung bình được tính theo công thức sau:
$\bar A = \frac{{\sum {{A_i}.{X_i}\% } }}{{\sum {{X_i}\% } }}$
Ví dụ:
Hãy tính nguyên tử khối trung bình của silic, biết rằng silic có các đồng vị với % số nguyên tử tương ứng như sau:
$_{14}^{29}Si\left( {4,67\% } \right);_{14}^{28}Si\left( {92,23\% } \right);_{14}^{30}Si\left( {3,10\% } \right)$
Hướng dẫn giải
Nguyên tử khối trung bình của $Si$ là:
$\overline {{A_{Si}}} = \frac{{\left( {28 \times 92,23} \right) + \left( {29 \times 4,67} \right) + \left( {30 \times 3,10} \right)}}{{100}} = 28,109.$
4. Bài tập áp dụng (xem file đính kèm)