Ứng dụng tích phân để tính diện tích hình phẳng
Được đăng bởi
06/11/2017 09:09
1. Công thức 1
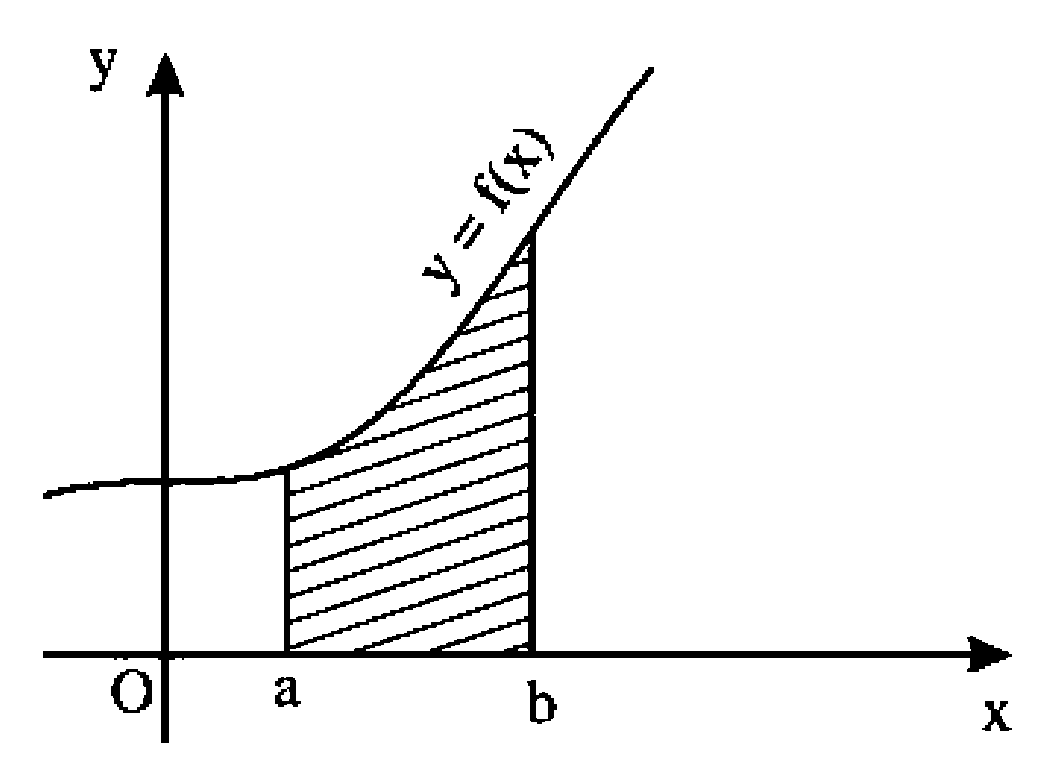
Nếu hàm số $y = f\left( x \right)$ liên tục trên đoạn $\left[ {a;b} \right]$ thì diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y = f\left( x \right)$, trục hoành và hai đường thẳng $x = a,x = b$ $\left( {a < b} \right)$ là:
$S = \int_a^b {\left| {f\left( x \right)} \right|} dx$
2. Công thức 2
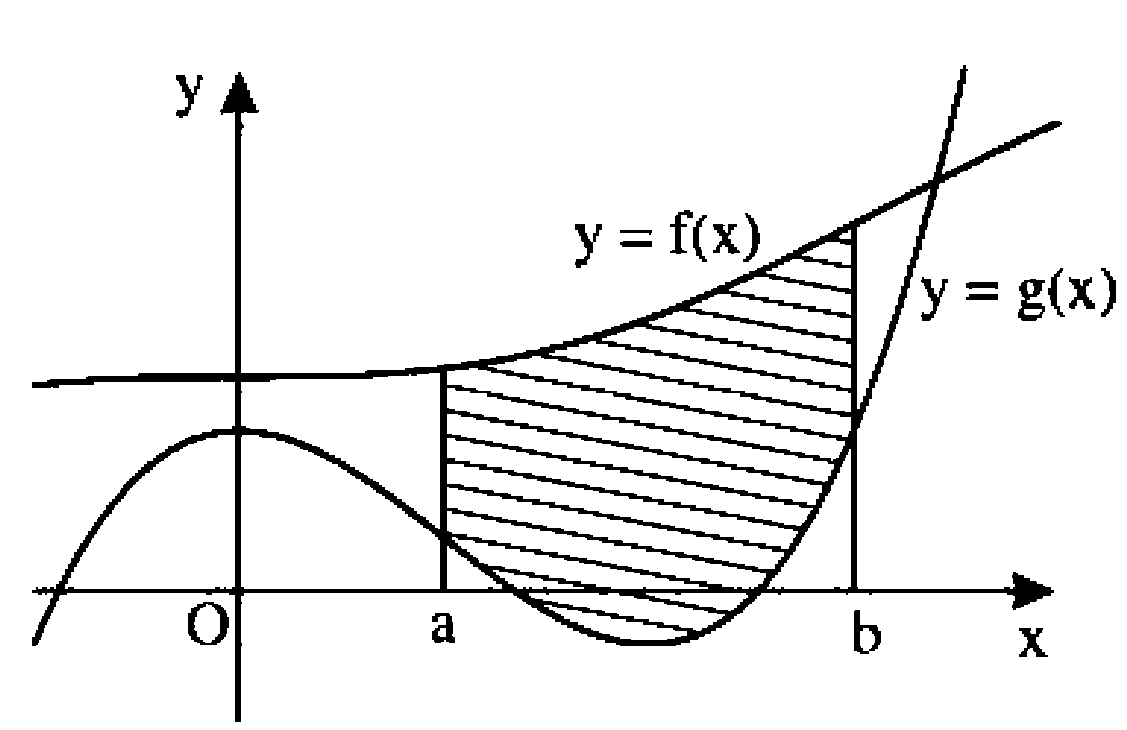
Nếu hàm số $y = f\left( x \right)$ và $y = g\left( x \right)$ liên tục trên đoạn $\left[ {a;b} \right]$ thì diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y = f\left( x \right)$, đồ thị $y = g\left( x \right)$ và hai đường thẳng $x = a,x = b$ $\left( {a < b} \right)$ là:
$S = \int_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|} dx$
3. Các dạng bài toán và phương pháp giải: (xem file bên dưới)



